Положим например 
. Интеграл
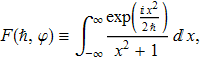
очевидно, сходится абсолютно (и равномерно относительно h>0) в силу оценки
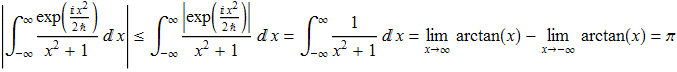
С другой стороны 
, что видно из разложения функции φ(x) в ряд Тейлора:
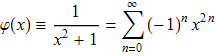
Подставляя эти производные в ФАР (Α), получим расходящийся ряд при всех h≠0
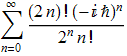
Его расходимость видна даже из признака Даламбера:
Тем не менее, возьмём 40 членов разложения асимптотического ряда (Α) и положим 
Теперь вычислим соответствующий интеграл численно:
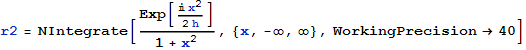
Абсолютная величина разности значений, вычисленных разными способами.
Приложение. Дельта-функция Дирака. Преобразование Фурье обобщённых функций.
1. Дельта-функцией Дирака δ(x) называется линейный непрерывный функционал над пространством D(R) основных (пробных) функций.
Функция ψ∈D(R), если:
1) Κ=supp[ψ]≡{x∈R: ψ(x)≠0} – компактное подмножество R (в данном случае это ограниченное замкнутое множество);
2) 
(R) – пространство бесконечно дифференцируемых финитных функций;
3) последовательность пробных функций 
(n=1,2,3,...) сходится к некоторой функции ψ∈D(R) тогда и только тогда, когда:
(a) существует компакт Κ, такой, что для любого n∈N 
;
(b) 
равномерно по x∈Κ.
Дельта-функция действует на пробную функцию ψ∈D(R) по правилу
2. Для преобразования Фурье обобщённых функций пространство пробных функций D не годится так оно не инвариантно относительно операции преобразования Фурье: F(D)≠D. Инвариантным относительно оператора F является пространство S. Это класс бесконечно диффкренцируемых функций на R и убывающих со всеми своими производными при x→∞ быстрее любой степени x. Формально, ψ∈S(R) тогда и только тогда, когда:
(a) 
(R);
(b) ∀ x∈R и ∀ α, β ∈N∪{0} ∃ 
, такая, что 
;
(c) последовательность функций 
(n=1,2,3,...) сходится к некоторой функции ψ∈S(R), если ∀α,β∈N∪{0}
равномерно по x∈R.
Дифференцирование обобщённых функций определяется так. Пусть f – обобщённая функция над пространством D или S. (будем иметь в виду S). Производной обобщённой функции f называется такой линейний непрерывный функционал 
над S, что ∀ ψ∈S выполняется равенство
И вообще, 
– это такая обобщённая функция, что
Скобки {f,g} означают интегрирование f g по R
Теперь мы можем показать, как вычисляется обратное преобразование Фурье функций 
, n∈N∪{0}.
Определим операторы преобразования Фурье по формулам
Преобразованием Фурье обобщённой функции g называется такая обобщённая функция F(g), что для любой функции ψ∈S(R) выполняется равенство
Будем считать 
обобщённой функцией. Тогда для любой 
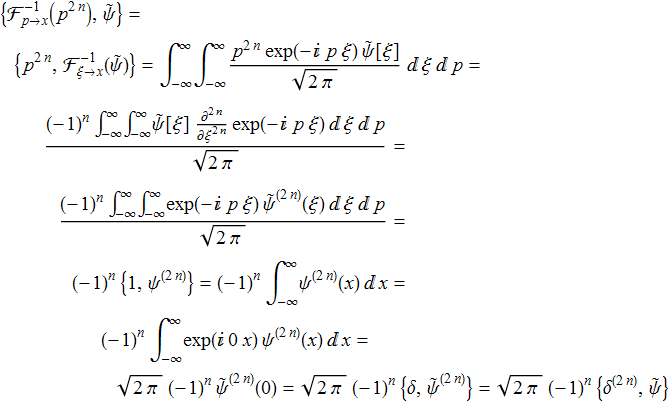
Сравнивая начало и конец выкладки, заключаем, что
Изложенный здесь метод является частным случаем метода стационарной фазы, который позволяет находить асимптотику интегралов вида
