Моделирование броуновского движения частицы. Винеровский случайный процесс. Предфрактальные множества.
1. Моделирование и визуализация траектории броуновской частицы на плоскости на небольшом интервале времени.
Определение (псевдо)случайного комплексного числа с модулем ρ и аргументом φ.
In[115]:=
In[44]:=
Генерация 30 (псевдо)случайных комплексных чисел.
In[136]:=
Вычисление списка частичных сумм элементов предыдущего списка lrns при помощи функции Accumulate
In[137]:=
Вычисление последовательности частичных сумм списка продемонстрируем на следующем примере. Пусть имеется список из 10 элементов
In[143]:=
Out[143]=
Применяя функцию Accumulate, получим список частичных сумм исходного списка:
In[145]:=
Out[145]//TableForm=
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Отображение 
, действующее по правилу z→{Re(z),Im(z)}, z∈C применяется к каждому элементу списка lpt
In[138]:=
Программирование стрелок.
In[139]:=
Код для построения графика.
In[142]:=
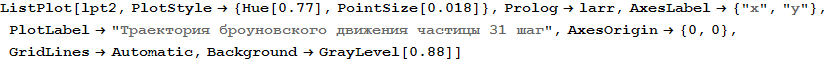
Out[142]=
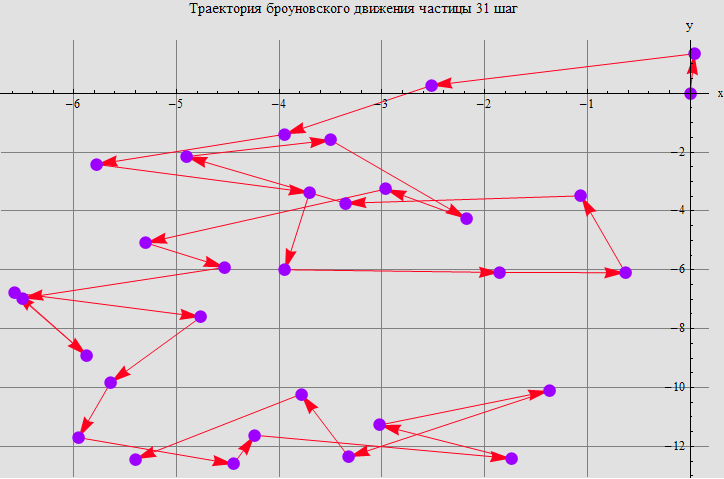
In[158]:=
2. Моделирование траектории движения броуновской частицы. Модуль ρ распределён равномерно на интервале (0, 0.1).
In[159]:=
In[160]:=
In[175]:=
In[176]:=
In[181]:=
Out[181]=
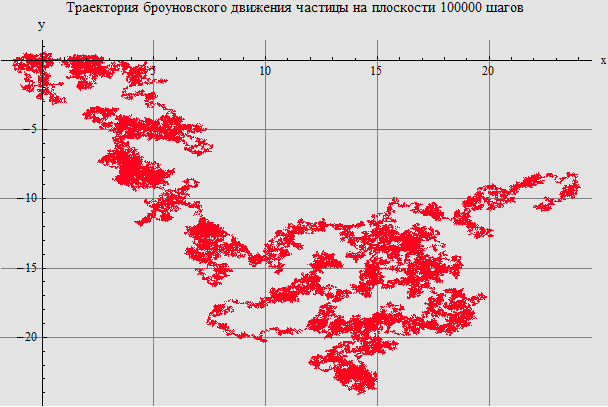
Броуновское движение описывается Винеровским случайным процессом. Очень интересным свойством Винеровского процесса является тот факт, что его траектории являются непрерывными функциями времени (в каждой точке) и при этом Винеровский процесс не дифференцируем по времени ни в одной точке. Траектории Винеровского процесса напоминают рисунок приведённый выше и представляют собой предфрактальное множество (фракталом называется множество с дробной размерностью по Хаусдорфу). Винеровский случайный процесс определяется при помощи ряда
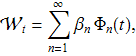
где 
– случайные величины, распределённые нормально, 
, 
, а
где функции 
образуют ортонормированную систему в 
. Можно доказать при помощи характеристических функций, что если взять ортонормированную тригонометрическую систему, то при фиксированном t плотность распределения вероятностей случайной величины 
является функция
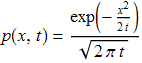
т. е. имеет нормальное распределение с мат. ожиданием 0 и дисперсией t.Кроме того, функция p(x,t) удовлетворяет задаче Коши для уравнения теплопроводности и диффузии
Рассмотрим малый фрагмент предыдущего рисунка в укрупнении (50 шагов).
In[187]:=
Out[187]=
3. Пусть теперь ρ распределена по закону Релея.
In[188]:=
In[190]:=
In[191]:=
In[192]:=
Out[192]=
