Ортогональное преобразование в 4-х мерном вещественном пространстве.
Создадим семейство однопараметрических ортогональных преобразований U(t) по формуле
где t∈R, а
, 
–нулевая и единичная матрицы 2×2.
In[1]:=
Out[1]//MatrixForm=
In[2]:=
Out[2]//MatrixForm=
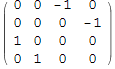
In[3]:=
Out[3]//MatrixForm=
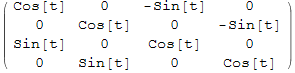
Проверяем ортогональность:
In[4]:=
Out[4]=
In[5]:=
Out[5]=
Групповое своиство:
In[6]:=
Out[6]=
Возьмём призвольный вектор 
In[8]:=
Out[8]=
Будем Будем поворачивать его с помощью U(Δt) на углы 0, Δt, 2Δt,...,9Δt
In[9]:=
In[10]:=
Out[10]=
Мы получили матрицу 10×4. Вычислим её ранг.
In[11]:=
Out[11]=
Это означает, что все строки этой матрицы лежат в одной плоскости (2-мерном подпространстве)
Определим 2 ортогональных вектора.
In[49]:=
Out[49]=
In[50]:=
Out[50]=
In[51]:=
Out[51]=
Определим символьный вектор
In[18]:=
Out[18]=
Составим систему из двух уравнений, которая описывает ортогональность вектора x векторам 
и 
In[52]:=
Out[52]=
Найдём решение этой системы.
In[53]:=
Out[53]=
In[54]:=
Out[54]=
На самом деле мы нашли плоскость, ортогональную плоскости, в которой лежат векторы 
и 
. Вот её уравнение в параметрической форме
In[55]:=
Out[55]//TraditionalForm=
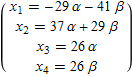
Найдём уравнение плоскости, в которой лежат векторы 
и 
в параметрическом виде.
In[56]:=
Out[56]=
In[57]:=
Out[57]//TraditionalForm=
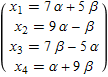
L и N представдяют собой плоскости (2-мепные подпространства) когда α и β пробегают всё R независимо друг от дпуга.
Эти плоскости ортогональны.
In[58]:=
Out[58]=
Плоскость L содержит все образы вектора 
при отображении U(t), t∈[0, 2π]. Они, конечно ортогональны плоскости N:
In[59]:=
Out[59]=
Вектор-функция U(t).
, t∈[0, 2 π] удовлетворяет системе дифференциальных уравнений
In[65]:=
Out[65]=
In[67]:=
Out[67]//TraditionalForm=
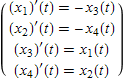
и начальным условиям Коши
In[68]:=
Out[68]=
In[69]:=
Out[69]//TraditionalForm=
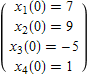
In[70]:=
Out[70]=
Найдём решение описанной выше задачи Коши
In[71]:=
Out[71]=
In[72]:=
Out[72]=
