Знакопостоянные квадратичные формы.
Лемма 1. Пусть A – симметричная (
) вещественная n×n матрица и det(A)≠0 Тогда любые два собственных вектора, отвечающих различным собственным значениям взаимно ортогональны.
Доказательство.
Пусть 
, 
– различные собственные выкторы, отвечающие различным собственным значениям 
и 
. Заметим, что среди собственных чисел нет нулевых. Тогда
Отсюда
Но 
. Поэтому 
.
Лемма 2. Если все собственные числа симметричной матрицы A положительны, то A>0 (положительно определена, т.е. для любого x≠0 {A x,x}>0)
Доказательство.
Согласно лемме 1, собственные векторы симметричной матрицы образуют ортогональный базис. Мы можем считать его ортонормированным: 
Пусть 
– произвольный (но ненулевой вектор) и пусть 
– его координаты в базисе состоящем из собственных векторов 
матрицы A. Тогда
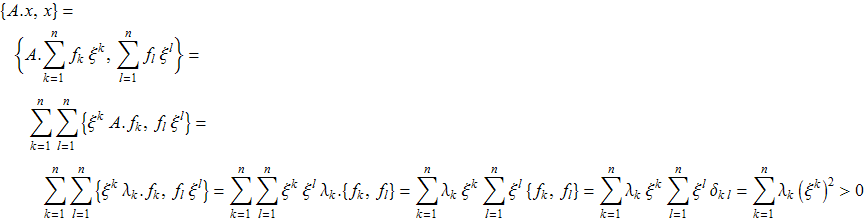
1. Построим ортогональную матрицу 6×6 
, где
где 
, 
– нулевая и единичные матрицы 3×3
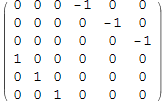
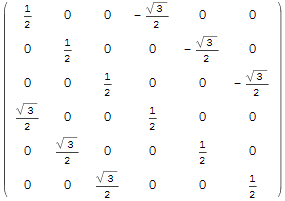
Проверка ортогональности матрицы U
Создаём диагональную матрицу с положительными числами.
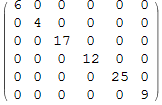
Создаём симметричную матрицу с положительными собственными значениями.
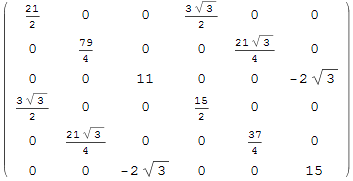
Проверяем симметричность.
Собственные значения:
Собственные векторы:
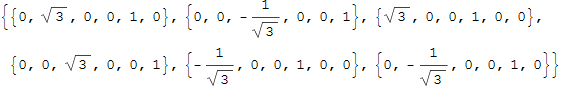
Матрица Грамма:
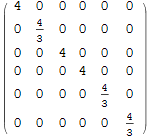
Вычисляем знаки последовательности главных миноров 
(k=1,2,...,6)
Все главные миноры положительны, следовательно матрица A>0 (положительно определена).
Определим квадратичную форму с матрицей A
Найдём её глобальный минимум
Интересный результат даёт функция Reduce
2. Отрицательные собственные значения.
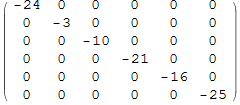
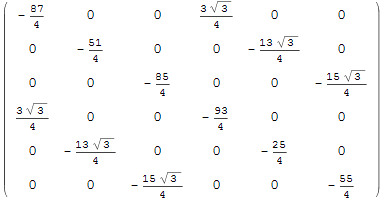
Собственные числа.
Знаки главных миноров чередуются, начиная с -1, значит A<0 (отрицательно определена)
Квадратичная форма с матрицей A:
Находим глобальный максимум:
