Функции от эрмитовых матриц.
Построение эрмитовой матрицы 5 ×5 со случайными числами из квадрата -9≤Re(z)≤9, -9≤Im(z)≤9.
1. Построение верхней треугольной матрицы (глапная диагональ нулевая).
In[1]:=
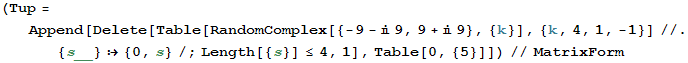
Out[1]//MatrixForm=
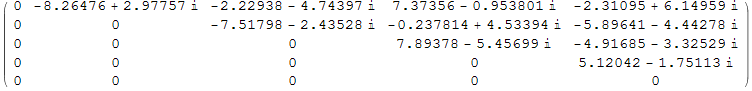
2. Применяем транспонирование и комплексное сопряжение.
In[2]:=
Out[2]//MatrixForm=
3. Строим диагональную матрицу (на глапной диагонали эрмитовой матрицы должны быть вещественные числа).
In[3]:=
Out[3]//MatrixForm=
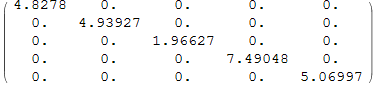
4. Сумма трёх предыдущих матриц даёт эрмитову матрицу.
In[4]:=
Out[4]//MatrixForm=
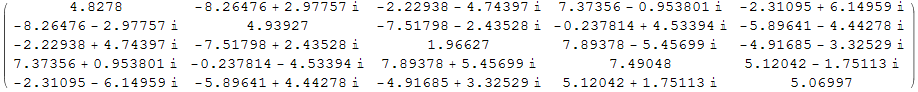
In[5]:=
Out[5]=
Проверяем,является ли полученная матрица эрмитовой?
In[6]:=
Out[6]=
Находим собственные числа:
In[7]:=
Out[7]=
Находим собственные векторы.
In[8]:=
Проверяем основные трждества: 
In[9]:=
Out[9]=
Собственные векторы нормированы:
In[10]:=
Out[10]=
Собственные векторы попарно ортогональны (все скалярные произведения 
, при i≠j)
In[11]:=
Out[11]=
Таким образом, собственные векторы 
образубт ортонормированный базис в 
. Матрица Грамма:
In[12]:=
Out[12]//MatrixForm=
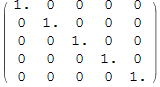
Пусть дан собственный вектор g
In[13]:=
Out[13]//MatrixForm=
Тогда проэктор на собственное подпространство, порождённое этим вектором строится так
In[14]:=
Out[14]//TraditionalForm=
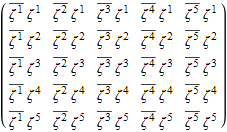
Проэкторы на собственные подпространства и их свойства.
Построение проэкторов на собственные подпространства, порождённые собственными векторами.
In[15]:=
In[16]:=
Out[16]=
Последнее вычисление показывает, что ранг каждого проэктора равен 1, а это означает, что все собственные подпространства одномерны.
Свойство 0. (a) Для любых j и k
Доказательство. Учитывая структуру проэкторов и ортонормированность системы собственных векторов, имеем
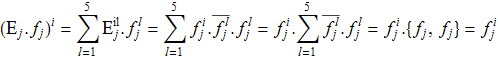
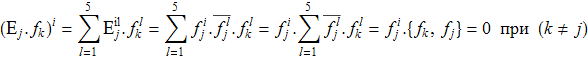
Проверим доказанные свойства:
In[17]:=
Out[17]=
In[18]:=
Out[18]=
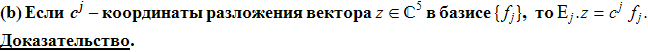
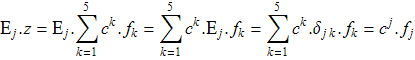
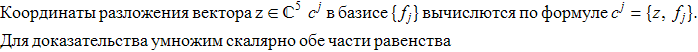
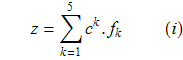
на 
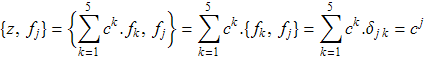
Возьмём вектор со случайными комплексными числами
In[19]:=
Out[19]=
Найдём координаты его разложения
In[20]:=
Out[20]=
Проверим тождество (i)
In[21]:=
Out[21]=
Проверим свойство 0 (b):
In[22]:=
Out[22]=
Найдём ранг матриц вида
In[23]:=
Out[23]//TraditionalForm=
In[24]:=
Out[24]=
Ранг всех таких матриц равен 2, а это означает, что вектор z не коллинеарен ни одному из собственных векторов 
матрицы A
Ещё одно подтверждение свойства 0 (b)
In[25]:=
Out[25]=
Это ознаяает, что 
проэктирует вектор z на прямую, содержащую вектор 
Свойство 1. Для любого j
Доказательство.
Для любого 
В силу произвольности выбора z, имеем
Далее,
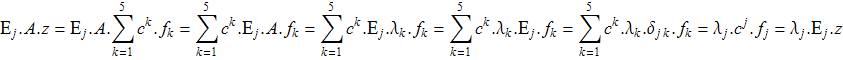
В силу произвольного выбора z
Доеазательство закончено. Провкрим сврйство 1 прямыми вычислениями.
In[26]:=
Out[26]=
In[27]:=
Out[27]=
Свойство 2. Импотентность проэкторов. Для любого j
Доказательство. Для любого 
В силу произвольноссти в выборе z, отсюда следует утверждение свойства 2.
Проверяем свойство 2 непосредственными вычислениями:
In[28]:=
Out[28]=
Свойство 3. При любых i, j, i≠j
Доказательство. Для любого 
Проверим это свойство прямыми вычислениями.
Поясним процедуру вычисления на символьном примере. Пусть имеется список из 5 матриц
In[29]:=
Out[29]=
Теперь нужно сформировать всевозможные пары с различными элементами, а это не что иное как множество всех двухэлементных подмножеств исходного множества.
In[30]:=
Out[30]=
Можно применить ккаждой паре абстрактную функцию f
In[31]:=
Out[31]=
Однако, нам нужно получить не функции от списка вида 
, а функции от пары аргументов 
. Для этого нужно использовать функцию замены заголовка
Apply (@@)
In[32]:=
Out[32]=
Теперь вместо f следует подставить функцию матричного умножения Dot
In[33]:=
После перемножения всех пар (а их 10) получен список из 10 матриц. Далее вычисляктся норма каждойй матрицы. Погрешность вычислений устраняется при помощи функции Chop
Свойство 4. Проэкторы эрмитовы т.е. для любого j
Доказательство. Для любого 
С другой стороны
Отсюда следует, что проэкторы самосопряжены, т.е. их матрицы эрмитьвы.
Проверяем доказанное свойство прямыми вычислениями.
In[34]:=
Out[34]=
Свойство 5. Имеет место тождество
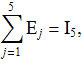
где 
– единичная матрица 5-го порядка.
Доказательство. Для любого 
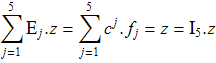
Проверка непосредственным вычислением
In[35]:=
Out[35]=
Свойство 6. (Следствие свойства 1 и свойства 5) . Имеет место тождество
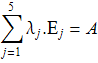
Доказательство.
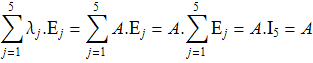
Проверяем прямым вычислением:
In[36]:=
Out[36]=
Свойство 7. Если T – произвольная матрица не коммутирующая с A, то матрица
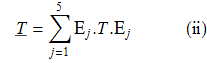
коммутирует с A. (Следствие свойства 1).
Доказательство.
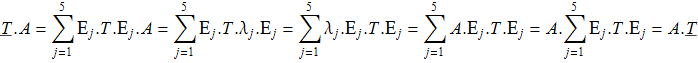
Создадим матрицу со случайными числами
In[37]:=
Вычислим норму коммутатора
In[38]:=
Out[38]=
Матрицы T и A не коммутируют. Вычислим матрицу 
по формуле (ii)
In[39]:=
Теперь видим, что матрица 
коммутирует с A
In[40]:=
Out[40]=
Определение функции от эрмитовой матрицы.
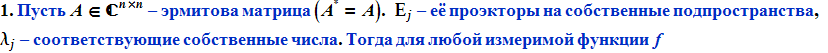
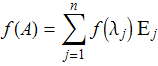
(Случай простого спектра).
2. Рассмотрим ещё одно определение функции от матрицы (необязательно эрмитовой). Пусть 
– все (различные) собственные значения матрицы A. Исходя из равенств
строится интерполяционный полином 
(узлами интерполяции являются собственные числа матрицы A).
Коэффициенты полинома 
(k=0,1,...,n-1) определяются из приведённой выше системы уравнений (iii). По определению полагают
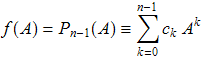
Докажем эквивалентность этих определений в случае эрмитовой матрицы с простым спектром. Используя свойства 6, 3, 2, имеем цепочку равенств:
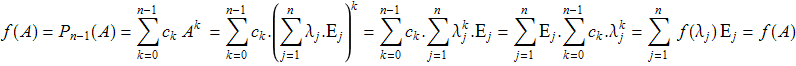
Примеры.
1. Определим, например матрицу cos(A)
In[41]:=
В системе Mathematica есть функция MatrixExp с помощью которой также можно вычислить cos(A). Сравним наше определение с определеием, вычисленным при помощи встроенной функции.
In[42]:=
Out[42]=
2. Определим косинус-матрицу с параметром cos(A t), t∈R
In[43]:=
Функции от матриц широко применяются в теории дифференциальных уравнений, теории возмущений, асимптотических методах.
Рассмотрим например систему дифференциальных уравнений
где z - вектор функция от t:
In[44]:=
Out[44]=
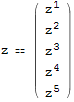
Возьмём произвольный вектор
In[45]:=
Out[45]//MatrixForm=
Тлгда вектор cos (A t).g удовлетворяет системе дифференциальных уравнений (iv):
In[46]:=
Out[46]=
In[47]:=
Out[47]=
При этом выполняются начальные условия Коши:
In[48]:=
Out[48]//TraditionalForm=
