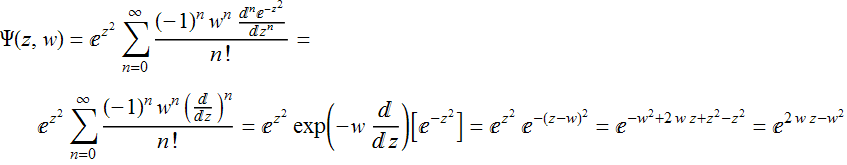Псевдодифференциальный оператор.
Операторный метод нахождения частного решения линейного дифференциального уравнения с полиномиальной правой частью в символьном виде.
Линейный дифференциальный оператор с постоянными коэффициентами 5-го порядка.
Полином в правой части уравнения 4-го порядка.
Пусть требуется найти частное решение уравнения
Построение соответственного характеристического полинома.
Найдём решение, применяя обратный оператор 
к правой части R
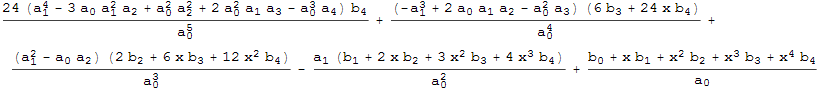
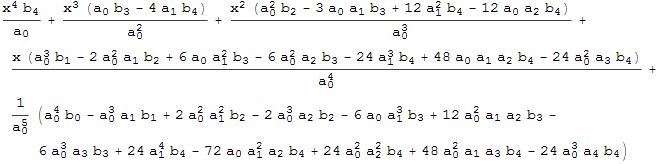
Проверяем, удовлетворяет ли полученное решение нашему уравнению.
Очевидно, выполняется тождество
Выполняется также тождество с операторами, действующими в обратном порядке.
Такой же пример, но в численном виде.
Линейный дифференциальный оператор с постоянными коэффициентами 3-го порядка.
Полином в правой части уравнения 10-го порядка.
Требуется найти частное решение уравнения
Построение соответственного характеристического полинома.
Найдём решение, применяя обратный оператор 
к правой части R
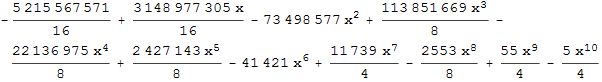
Проверяем, удовлетворяет ли полученное решение нашему уравнению.
Очевидно, выполняется тождество
Выполняется также тождество с операторами, действующими в обратном порядке.
Выясним, какой задаче Коши удовлетворяет полученное решение.
Это начальные условия Клши, отвечающее полученному решению.
Псевдодифференциальные уравнения с полиномиальной правой частью.
1. Рассмотрим псевдодифференциальное уравнение, где правая часть R(x) –полином 10-порядка.
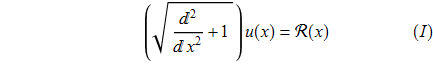
Разложим функцию
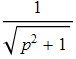
в ряд Тейлора до 10-го порядка включительно (остаток в форме 
) так как 11-ая производная R(x)равна нулю:
Заменим каждый член разложения 
оператором дифференцирования 
и применим полученный оператор к R.
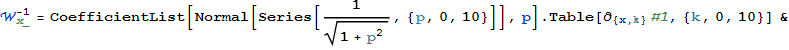
Находим решение.
Проверим правильность решения.
Если вместо R взять экспоненту exp(x), то так как
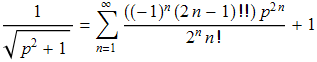
а 
, то
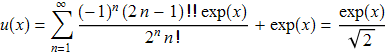
2. Рассмотрим псевдодифференциальный оператор
Выясним, как он деёствует на произвольную функцию u(x). Положим
Дифференцируя функцию v(x,t) по t, получим
Имеем Задачу Коши
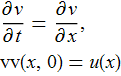
Она легко решается, например, методом характермстик. Её решение
Таким образом, данный псевдодифференциальный оператор действует на функцию прибавляя к её аргументу t. Он называется оператором сдвига.
Вообще, для некоторого специального класса функций, псевдодифференциальный оператор (функция от дифференциального оператора) определяется по формуле
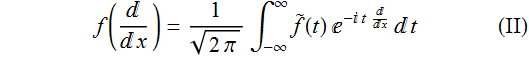
где 
– преобразование Фурье функции f. Найдём решение псевдодифференциального уравнения (I), используя формулу (II)/
Находим преобразование функции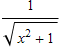 
Применяем оператор (II) к правой части R(x). Учитывая правило, по которому деёствует оператор сдвига, получим
Сравниваем с ранее полученным результатом.
Если вместо R(x) взять 
, получим u(x) в качестве решения (I)
3. Рассмотрим псевдодифференциальный оператор
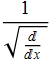
Это оператор интегрирования дробногй кратности (в данном случае 
-кратное интегрирование).. Используя формулу (II) применим его к функции 
. Сначала найдём Фурье-образ символа этого оператора.
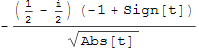
Теперь применяем орератор (II) к функции 
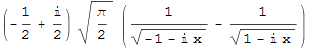
Это результат 
-кратного интегрирования. Применим к полученной функции ещё раз оператор (II)
Эта функция лишь на константу отличается от arctag(x) и является первообразной от 
. Проверка дифференцированием:
4. Используя оператор сдвига можно найти производящую функцию для полиномов Эрмита, просуммировав ряд
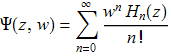
Полиномы Эрмита можно определить по формуле
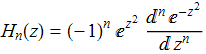
Подставляя это выражение в ряд, получим
