Евклидово пространство вещественных матриц.
Рассмотрим для примера матрицу A 3×3 со случайными элементами – целыми числами от –9 до 9. Найдём сначала ядро оператора коммутации с A (он называется 
).
In[1]:=
Out[1]//MatrixForm=
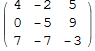
In[2]:=
Out[2]=
Определим нулевую матрицу 3×3:
In[15]:=
Out[15]//MatrixForm=
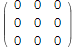
Определим вектор 
в символьном виде:
In[3]:=
Out[3]=
Построим из него матрицу 3×3:
In[4]:=
Out[4]//MatrixForm=
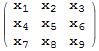
Определим функцию, вычисляющюю коммутатор:
In[5]:=
Вычислим коммутатор [A, X]:
In[6]:=
Out[6]=
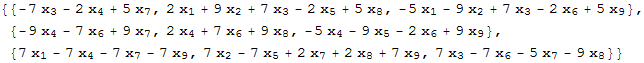
Коммутатор C=[A, X] содержит девять элементов. Мы их разупорядочим так, чтобы получилось 9 элементов одного списка:
In[7]:=
Out[7]=
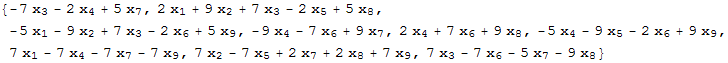
Рассмотрим 1-ый элемент полученного списка:
In[8]:=
Out[8]=
Он имеет вид c.x, где 
– вектор числовых коэффициентов. Найдём этот вектор.
In[9]:=
Out[9]=
Теперь заменим 1 на k и заставим его принимать все значения от 1 до 9. Получим некоторую матрицу M размнром 9×9:
In[10]:=
Out[10]//MatrixForm=
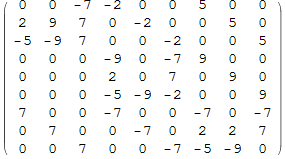
Эта матрица является матрицей системы уравнений для определения коммутатора [A, X]. Проверка ниже:
In[11]:=
Out[11]=
In[12]:=
Out[12]=
Ранг матрицы M равен 6, а это означает, что пространство решений уравнения M.x=0 (корневое подпространство) имеет размерность 3.
Найдём базис корневого подпространства матрицы M:
In[13]:=
Out[13]=
Образуем линейную оболочку этих векторов:
In[16]:=
Out[16]=
In[17]:=
Out[17]=
Образуем из этого вектора матрицу, разбивая его на три строки:
In[18]:=
Out[18]//MatrixForm=
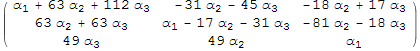
Это и есть ядро оператора коммутирования с A (на самом деле это общий вид матрицы коммутирующей с A).
Проверяем коммутативность A с K:
In[19]:=
Out[19]=
Определим скалярное произведение в линейном пространстве вещественных матриц по формуле
Докажем, что определение (1) корректно, т.е. выполнены все аксиомы скалярного произведения.
1. Для любой A
причём {A,A}=0 ⇔ A=0. Действительно,
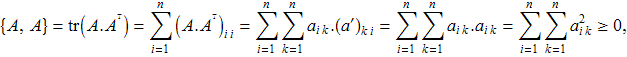
где через 
обозначены элементы транспонированной матрицы. В последней сумме учавствуют все элементы матрицы A в квадрате, поэтому равенство нулю возможно тогда и только тогда, когда все элементы матрицы A равны 0, т.е. A=0.
2. Линейность по первому аргументу. Для любых матриц 
, 
, B и для любых чисел 
, 
3. Симметричность. Для любых A, B
Учитывая свойство матриц
и тот факт, что при транспонировании матрицы её след не меняется, имеем:
Линейность по второму аргументу следует из свойства 3 и 2.
Определим функцию, вычисляющюю скалярное произведение по формуле (1):
In[21]:=
Определим норму исходя из скалярного произведения:
In[22]:=
Возьмём какую-нибудь матрицу (со случайными числами)
In[23]:=
Out[23]//MatrixForm=
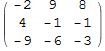
Тогда S=[A, T]∈
(принадлежит образу оператора 
).
In[24]:=
Out[24]//MatrixForm=
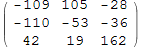
Вычислим квадрат расстояния от 
до 
In[25]:=
Out[25]=
Найдём проэкцию S на 
. Для этого найдём минимальное значение form и значения 
(k=1,2,3), при которых этот минимум достигается.
In[27]:=
Out[27]=
Назовём проэкцию S на 
через P:
In[29]:=
Out[29]=
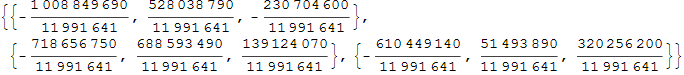
Вектор, начало которого в P а конец в S назовём через H:
In[30]:=
Out[30]=
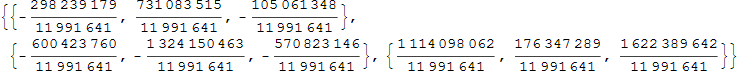
Длина перпендикуляра, опущенного из S на 
равна норме H и равна минимальному значению form:
In[31]:=
Out[31]=
Матрица H ортогональна 
:
In[33]:=
Out[33]=
Проверим, верна ли теорема Пифагора для прямоугольного треугольника SOP ?:
In[34]:=
Out[34]=
Найдём сумму острых углов треугольника SOP в градусах:
In[37]:=
Out[37]=
Проверим ещё тождество параллелограмма: Для параллелограмма ABCD выполнено тождество:
Определим три случайные матрицы A, B и C:
In[40]:=
Out[40]=
In[41]:=
Out[41]=
Определим векторы, образующие стороны параллелограмма:
In[43]:=
Out[43]//MatrixForm=
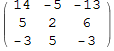
In[44]:=
Out[44]//MatrixForm=
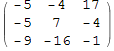
Определим векторы, образующие диагонали параллелограмма:
In[45]:=
Out[45]//MatrixForm=
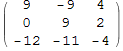
In[46]:=
Out[46]//MatrixForm=
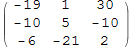
Проверяем тождество параллелограмма:
In[47]:=
Out[47]=
