Часть I.
Операторный метод усреднения.

1. Даны две эрмитовы матрицы A и B,  [A,B]≠0,  ε>0  – малый параметр (ε → 0).
Требуется найти такое унитарное преобразование U=U(ε), чтобы выполнялось тождество

и при этом

Если соотношения (1), (2) будут выполнены, то для любой допустимой функции f  будет выполнено тождество

Это утверждение называется леммой о квазикоммутации.

Лемма 1. Пусть выполняется равенство

Тогда для любого допустимрго f

Доказательство.

Но

Здесь числа над операторами означают порядок их действия.  Исползовалось также тождество, связанное с разностной производной

В частности

Это позволяет исследовать поведение траекторий автономных систем линейных дифференциальных уравнений с постоянными коэффициентами (матрица коэффициентов A+ε B) при больших временах t ∼1/ε, когда ε→0.

2. Унитарное преобразование U(ε) будем искать в виде

где C=C(ε) – антиэрмитова матрица:

Тогда U=U(ε) будет унитарной. Действительно,

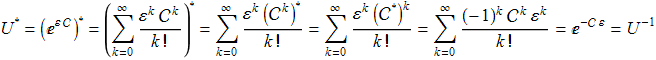
Далее нам потребуется следующая
Лемма 2.

где –оператор коммутирования с C:

Доказательство.

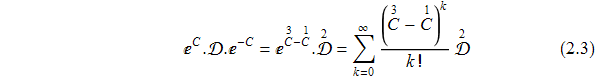
При k=1 имеем

Пусть при k=n

Тогда при k=n+1 будем иметь

Продолжаем цепочку равенств (2.3)

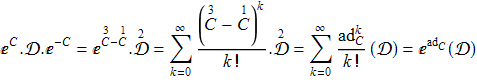
Перепишем тождество (1.1) с учётом (2.1) и леммы 2 в виде

Матрицы C и будем искать в виде

Подставляем (2.5), (2.6) в (2.4) и разлагаем левую часть (2.4) в ряд и приравниваем коэффициенты при одинаковых степенях ε. В результате получим три уравнения:

Используя свойства коммутатора перепишем данную систему уравнений в виде:

Кроме того имеется ещё три уравнения:

3. Пусть (j=1,...,n) – все различные собственные числа матрицы A и – соответствующие проэкторы на собственные подпространства. Напомним свойства проэкторов.

Проэкторы на собственные подпространства определяются так. Если z– собственный вектор матрицы A

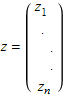
то проэктор на собственное подпространство, порождённое собственным вектором z есть такая матрица
}, что

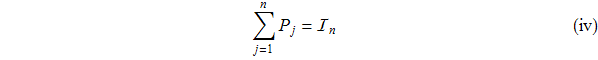
Следствие (i) и (iv):

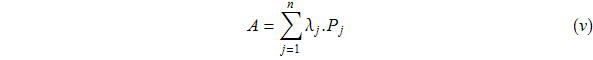
Введём в линейном пространстве матриц скалярное произведение по формуле

Для любых T,S∈. Tr – след матрицы.
Лемма 3.

Доказательство.

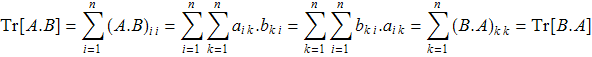
3.1. Лемма 4.  Оператор коммутирования   самосопряжён относительно скалярного произведения (3.1)
Доказательство.
Для любых T,S∈

С другой стороны

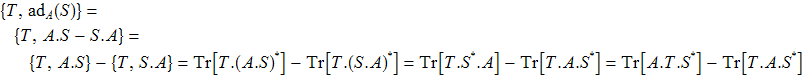
Сравнивая две цепочки равенств, получаем

3.2. Для любой матрицы T∈ определим матрицу по формуле

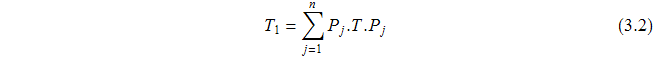
где – проэкторы на собственные подпространства A.
Лемма 5. коммутирует с А:

Доказательство следует из свойства (i) проэкторов:

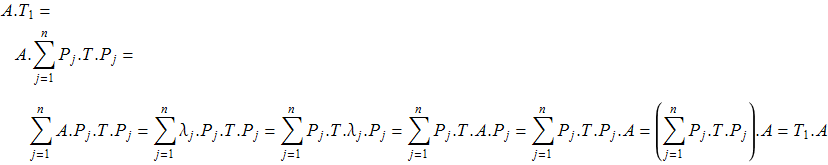
3.3. Лемма 6. Ядро оператора ортогонально его образу (относительного скалярного произведения (3.1)).
Доказательство. Возьмём произвольную матрицу S. Тогда [A,S]=. Возьмём произвольную матрицу . Поскольку оператор самосопряжён, имеем

3.4. Для любой матрицы T∈ определим матрицу по формуле

где суммирование распространяется по всем индексам j,k∈{1,2,...,n} и таких, что j≠k (всего (n-1) n слагаемых).
Лемма 7.  
Доказательство. Спроэцируем на

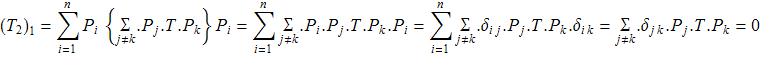
Это означает что ортогонально и значит .

Приведём ещё другое доказательство. Для любых S,T∈ определим матрицы , по формулам (3.2), (3.3) соответственно:

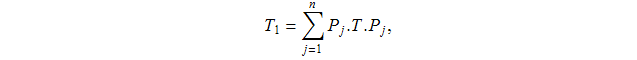
Доказано, что . Вычислим скалярное произведение

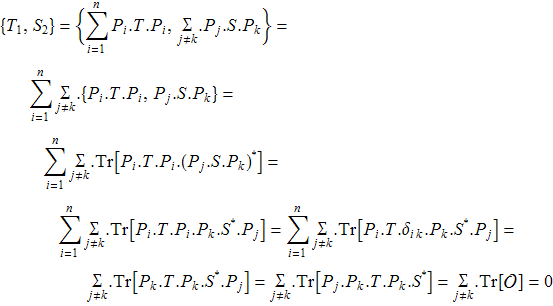
ортогональна и значит .

4. Определим индексное множество

Далее определим проэкторы на собственные подпространства оператора по формулам

для любой T.

Лемма 8. Проэкторы на собственные подпространства оператора обладают следующими свойствами:

Следствие (I) и (IV)

Докажем свойства (I) и (IV)

(I). Для любой T и μ≠0

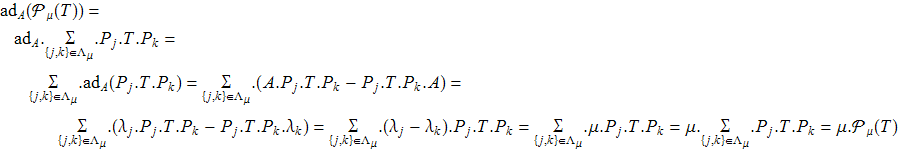
С другой стороны

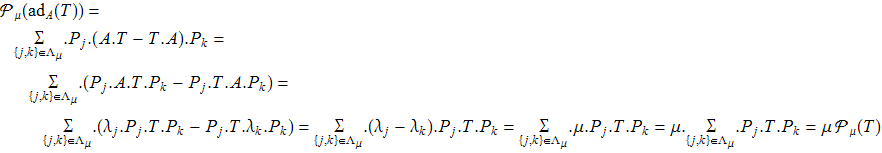
(IV)  Для любой T

Потому что , а  , а  образ и ядро ортогональны.

5. Вернёмся к системе уравнений при (k=1,2,3)  и (2.7)
Положим

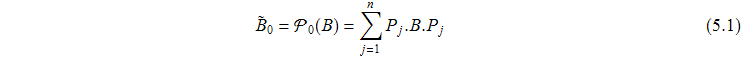
Тогда уравнение при можем записать в виде

Правая часть уравнения (5.2) принадлежит . Значит оно может быть разрешено относительно . Обозначим сужение оператора на подпространство L через . Из леммы 8 (I) имеем

На подпространстве L

Следовательно, на L

Это позволяет написать решение уравнения (5.2)

Таким образом находим по формуле

Положим

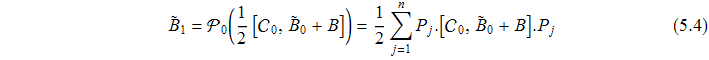
Перепишем уравнение при в виде

Правая часть последнего уравнения принадлежит ядру оператора коммутирования с A. Рассуждая аналогично, находим

Положим

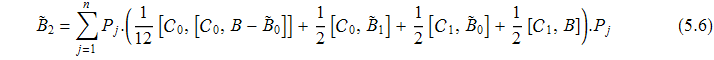
Тогда

Система уравнений при (k=1,2,3), (2.7) полностью решена. Тем самым представление (1.1) найдено с точностью до .

   Проверка выведенных формул на численном примере.

Задаём эрмитовы матрицы A и B  5×5.

In[1]:=

Out[1]//MatrixForm=

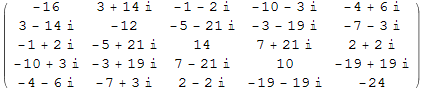
Проверяем, является матрица эрмитовой:

In[2]:=

Out[2]=

In[3]:=

Out[3]//MatrixForm=

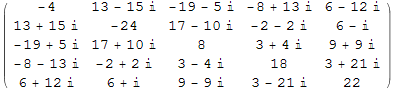
In[4]:=

Out[4]=

Находим собственные числа матрицы A.

In[5]:=

Out[5]=

Находим собственные векторы матрицы A

In[6]:=

Проверяем, является ли система собственных векторов ортонормированной.

In[7]:=

Out[7]=

Вычисляем проэкторы на собственные подпространства матрицы A:

In[8]:=

Определяем функцию для вычисления коммутатора

In[9]:=

Определяем нулевую матрицу 5×5:

In[10]:=

Out[10]//MatrixForm=

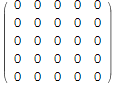
Вычисляем по формуле (5.1) как проэкцию матрицы B на

In[11]:=

Проверяем выполнение уравнения (2.7) при k=0:

In[12]:=

Out[12]=

Теперь нам предстоит вычислить по формуле (5.3):

Покажем как это можно сделать при помощи символов.
Определим символы проэкторов и собственных значений:

In[13]:=

Out[13]=

In[14]:=

Out[14]=

Сформируем список всех пар вида гдеj≠k. Это ничто иное как все 2х-элементные подмножества множества всех проэкторов p:

In[15]:=

Out[15]=

Однако к этому списку нужно ещё присоединить такой же список пар, но в обратном порядке:

In[17]:=

Out[17]=

Соеденим эти два списка:

In[18]:=

Out[18]=

Теперрь между проэкторами (на вторую позицию) нужно вставить матрицу b:

In[19]:=

Out[19]=

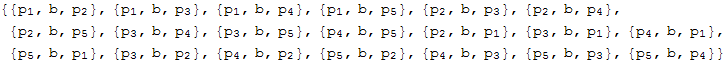
Затем нужно  перемножить все тройки матричным умножением. Для этого заменим заголовок каждой тройки List на функцию матричного умножения dot (пока dot – это просто символ):

In[20]:=

Out[20]=

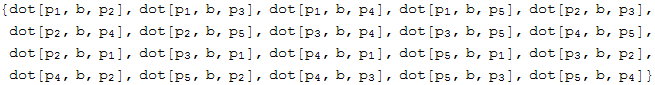
Мы получили список всех матриц вида при j≠k, входящих в сумму (5.3). Теперь найдём список всех коэффициентов, входящих в сумму (5.3). Список всех пар в прямом и обратном порядке находим аналогично:

In[21]:=

Out[21]=

Теперь заменим заголовок List каждой пары на заголовок функции :

In[23]:=

Out[23]=

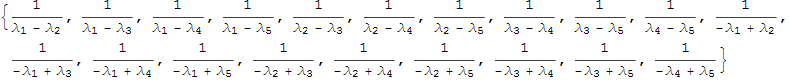
Теперь для получения суммы (5.3)  остается умножить скалярно вектор коэффициентов и вектор матриц:

In[24]:=

Out[24]=

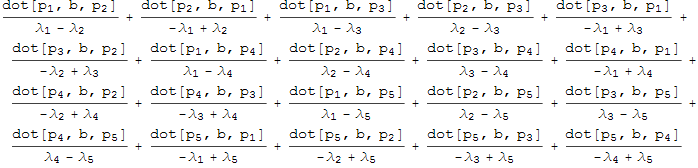
Сумма (5.3) вычислена в символическом виде. Процедура её вычисления  в стандартном виде выглядит так:

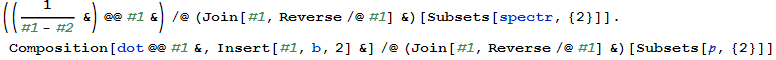
Теперь вместо символов подставляем реальные объекты и функции и вычисляем :

In[25]:=

Проверяем выполнение написанного выше уравнения:

In[26]:=

Out[26]=

Вычисляем по формуле (5.4)

In[27]:=

  Проверяем выполнение уравнения (2.7) при k=1

In[28]:=

Out[28]=

Вычисляем по формуле  (5.5):

In[29]:=

  Проверяем написанное выше тождество:

In[30]:=

Out[30]=

Вычисляем матрицу по формуле (5.6):

In[31]:=

In[32]:=

  Проверяем выполнение уравнения (2.7) при k=2

In[33]:=

Out[33]=

Вычисляем матрицу по формуле (5.7):

In[34]:=

Проверяем выполнение написанного выше уравнения:

In[35]:=

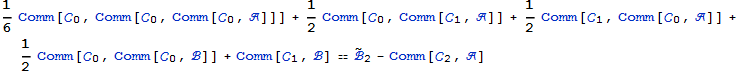
Out[35]=

Таким образом найдено представление (1.1) с точностью до

Матрицы , (k=0,1,2) коммутируют между собой:

In[36]:=

Out[36]=

Матрицы (k=0,1,2) антиэрмитовы:

In[37]:=

Out[37]=

Матрицы , (k=0,1,2) эрмитовы:

In[38]:=

Out[38]=

Матрицы ортогональны матрицам Матрицы , (i, j=0,1,2)

In[39]:=

Out[39]=

Матрицы так как их проэкция на равна 0.

In[40]:=

Out[40]=

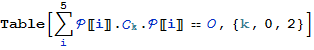
Created with Wolfram Mathematica 7.0